Want to find how far you can see from a certain location? Or how high you need to be to see 100 miles? Drag the human icon to a new location. Drag the pushpin to make select a point you want to see. The map will recenter when you are done.
More about this map
I love a good mapping problem so I set about gathering resources for this page. I started writing the mapping portion using the Google Maps 3.0 API with a little help from Abhinay Rathore [web3o.blogspot.com] I had to dig a little bit to rework Pythagoras' Theorem to figure out this problem but the calculation is pretty simple.
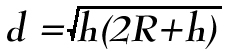
That's it really. There are a couple of different ways to solve this problem. Here, d is the distance to the horizon, h is your height off the ground, and R is the radius of the planet your standing on, presumably Earth at first. A huge assumption in all this is that there are no hills, trees or mountains blocking your horizon view. That's not to say that the world is flat though. Featureless, perhaps. The real trick on this and my aha, is that the right angle is not at the center of the planet but at the very horizon point you are looking at. It's at that point that a right angle is formed from the lines running to the viewer and to the center of the body.
So assuming you are a normal human alien and your eyes are about 5'7" off the ground (about 1.7 meters), your horizon is about 4.66 km away. The map starts here. On a smaller body, the Moon for instance, with a radius of only about 1737.5 km, the horizon is just 2.43 km away. Pretty close. While on a huge body likethe Sun, you'd see a whopping 34.4 km to the horizon. And this makes sense. On a larger celestial body with much more surface area, you'd see farther to the horizon. What I find interesting is our human perspective. From NASA reports, astronauts had a hard time gauging distances on the Moon. With a lack of known reference points, the horizon on the Moon is a tricky mistress. Our brains are hardwired to use visual cues such as shadows and haze to give us a sense of dimension and distance.
Suggestions for improvements to this? Drop me an email at john@terrazoom.com